算法之二分查找

二分查找思想

二分查找思想

   说之前我们先来玩个游戏《猜数字》，我规定范围0-100，并随机抽取一个数字63，剩下的人猜数字谁要是猜中了我随机抽取的数字63就要受罚！ 假如第一个人猜65，我说大了，那么第二个人就要猜比65小的。第二个人猜33，我说小了，第三个人就要猜比33大的。第三个人猜62，我说小了 那么凑巧走到第三个人就已经很刺激了，比62大比65小，那就是[63,64]两个数字了。剩下的人靠运气喽！
   二分查找又叫折半查找，是一种有序查找算法，必须先排序后查找！ 将首尾两位各自定义一个指针，计算出一个折半位置mid 将给定值target与折半位置mid比较有以下三种情况:
给定数组 nums[5,6,7,9,10,14,15,56]，给定target[15] 首指针为0（下标），尾指针nums.length-1，折半位置 (left + right) >>> 1

1. target > mid
   当给定值target大于折半位置mid，说明你要找的值肯定在mid右半部分。所以我们把首指针指到(mid+1)位置缩小查找范围。 
2. target < mid
   当给定值target小于于折半位置mid，说明你要找的值肯定在mid左半部分。所以我们把尾指针指到(mid-1)位置缩小范围。 
3. target = mid
   正好等于，直接返回

动态二分查找图

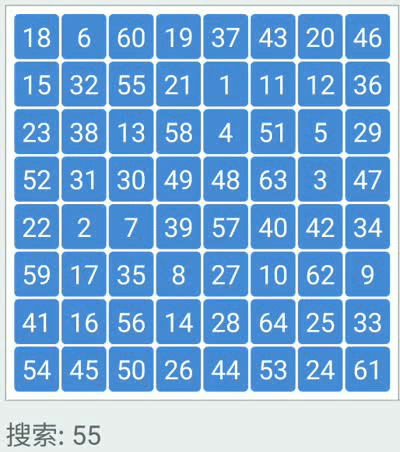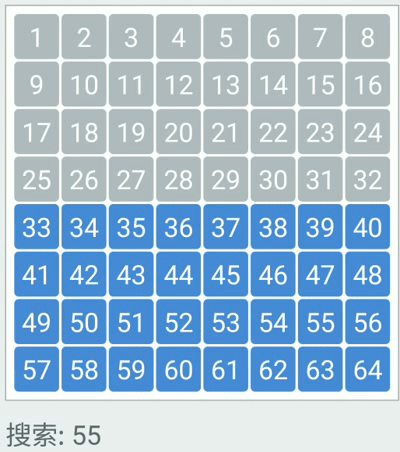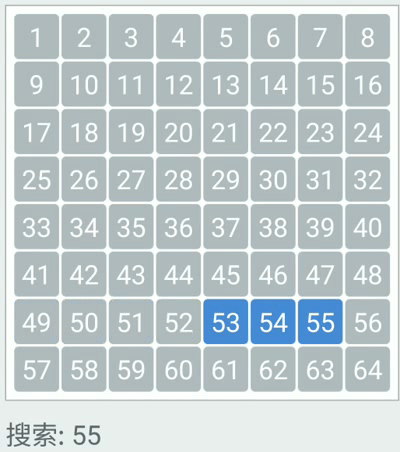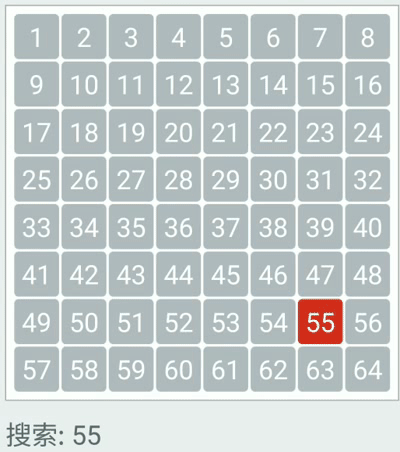
具体代码实现

Java

    public static int twoSelect(int[] nums, int target) {
    // 首指针
    int left = 0;
    // 尾指针
    int right = nums.length - 1;
    // 边界 首指针 <= 尾指针
    while (left <= right) {
        int mid = (left + right) >>> 1;
        if (target == nums[mid]) {
            return mid;
        }
        if (target > nums[mid]) {
            left = mid + 1;
        }
        if (target < nums[mid]) {
            right = mid - 1;
        }
    }
    return -1;
}

Python

https://pan.baidu.com/s/1pHP2QulSthS7PhKnNeQsyA?pwd=1475

总结

二分查找

    二分查找的时间复杂度是:O(logn) n就是数组的长度，空间复杂度O(1)，在大量有序数据中查找特定的值是一个不错的选择。